Chapter 14 PCA in R
Let’s find Principal Components using the iris dataset. This is a well-known dataset, often used to demonstrate the effect of clustering algorithms. It contains numeric measurements for 150 iris flowers along 4 dimensions. The fifth column in the dataset tells us what species of Iris the flower is. There are 3 species.
- Sepal.Length
- Sepal.Width
- Petal.Length
- Petal.Width
- Species
- Setosa
- Versicolor
- Virginica
Let’s first take a look at the scatterplot matrix:
pairs(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,data=iris,col=c("red","green3","blue")[iris$Species])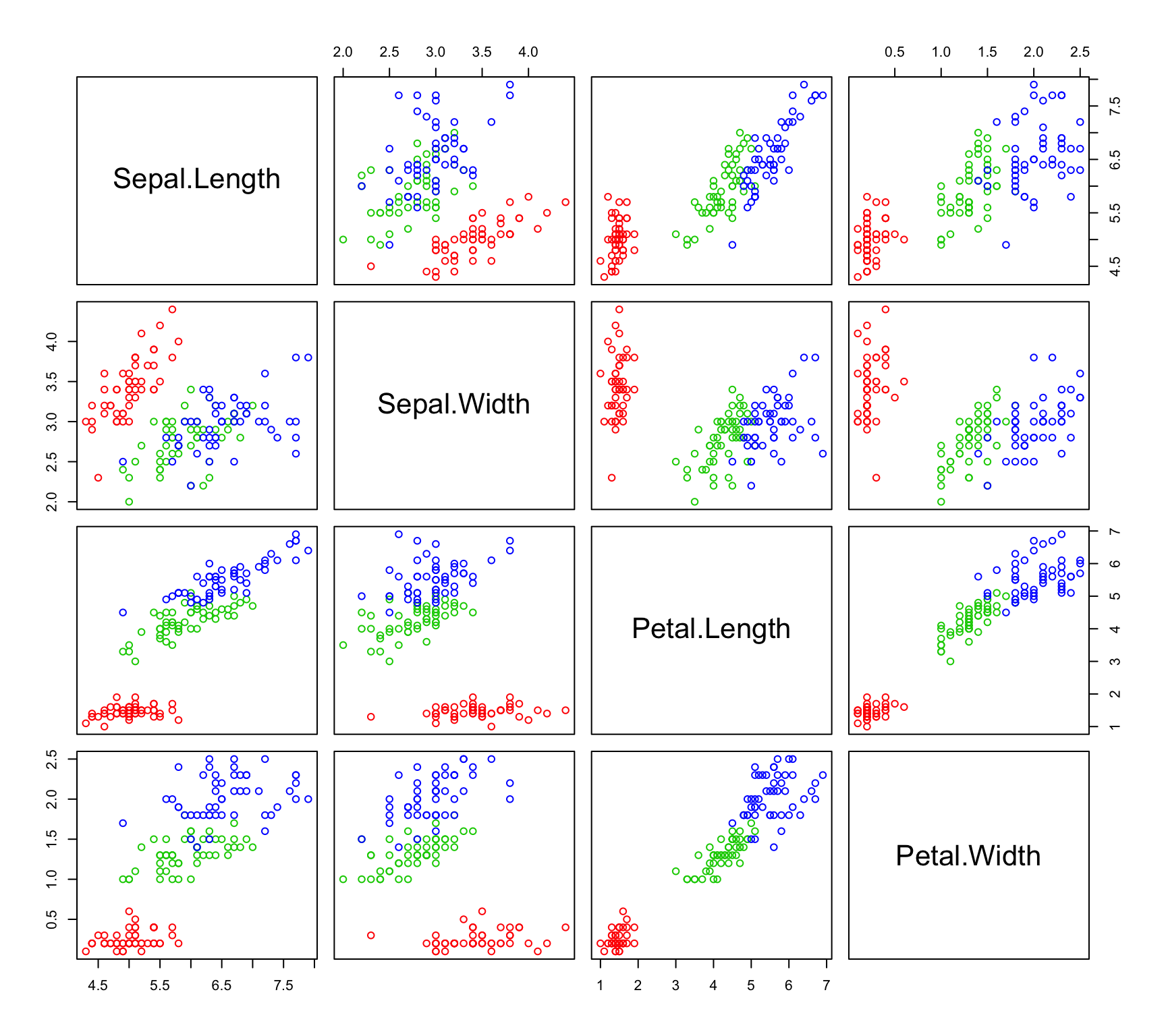
It is apparent that some of our variables are correlated. We can confirm this by computing the correlation matrix with the cor() function. We can also check out the individual variances of the variables and the covariances between variables by examining the covariance matrix (cov() function). Remember - when looking at covariances, we can really only interpret the sign of the number and not the magnitude as we can with the correlations.
cor(iris[1:4])## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
## Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
## Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
## Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000cov(iris[1:4])## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length 0.6856935 -0.0424340 1.2743154 0.5162707
## Sepal.Width -0.0424340 0.1899794 -0.3296564 -0.1216394
## Petal.Length 1.2743154 -0.3296564 3.1162779 1.2956094
## Petal.Width 0.5162707 -0.1216394 1.2956094 0.5810063We have relatively strong positive correlation between Petal Length, Petal Width and Sepal Length. It is also clear that Petal Length has more than 3 times the variance of the other 3 variables. How will this effect our analysis?
The scatter plots and correlation matrix provide useful information, but they don’t give us a true sense for how the data looks when all 4 attributes are considered simultaneously.
In the next section we will compute the principal components directly from eigenvalues and eigenvectors of the covariance or correlation matrix. It’s important to note that this method of computing principal components is not actually recommended - the answer provided is the same, but the numerical stability and efficiency of this method may be dubious for large datasets. The Singular Value Decomposition (SVD), which will be discussed in Chapter 16, is generally a preferred route to computing principal components. In fact, the numerical computation of principal components is outside of the scope of this book. We recommend [@cite1,@cite2, or @cite3] for a treatment of the topic. using both the covariance matrix and the correlation matrix, and see what we can learn about the data. Let’s start with the covariance matrix which is the default setting for the prcomp function in R.
14.0.1 Covariance PCA
Let’s start with the covariance matrix which is the default setting for the prcomp function in R. It’s worth repeating that a dedicated principal component function like prcomp() is superior in numerical stability and efficiency to the lines of code in the next section. The only reason for directly computing the covariance matrix and its eigenvalues and eigenvectors (as opposed to prcomp()) is for edification. Computing a PCA in this manner, just this once, will help us grasp the exact mathematics of the situation and discover the nuances of them.
14.0.2 Principal Components, Loadings, and Variance Explained
covM = cov(iris[1:4])
eig=eigen(covM,symmetric=TRUE,only.values=FALSE)
c=colnames(iris[1:4])
eig$values## [1] 4.22824171 0.24267075 0.07820950 0.02383509rownames(eig$vectors)=c(colnames(iris[1:4]))
eig$vectors## [,1] [,2] [,3] [,4]
## Sepal.Length 0.36138659 -0.65658877 -0.58202985 0.3154872
## Sepal.Width -0.08452251 -0.73016143 0.59791083 -0.3197231
## Petal.Length 0.85667061 0.17337266 0.07623608 -0.4798390
## Petal.Width 0.35828920 0.07548102 0.54583143 0.7536574The eigenvalues tell us how much of the total variance in the data is directed along each eigenvector. Thus, the amount of variance along \(\mathbf{v}_1\) is \(\lambda_1\) and the proportion of variance explained by the first principal component is \[\frac{\lambda_1}{\lambda_1+\lambda_2+\lambda_3+\lambda_4}\]
eig$values[1]/sum(eig$values)## [1] 0.9246187Thus 92% of the variation in the Iris data is explained by the first component alone. What if we consider the first and second principal component directions? Using this two dimensional representation (approximation/projection) we can capture the following proportion of variance: \[\frac{\lambda_1+\lambda_2}{\lambda_1+\lambda_2+\lambda_3+\lambda_4}\]
sum(eig$values[1:2])/sum(eig$values)## [1] 0.9776852With two dimensions, we explain 97.8% of the variance in these 4 variables! The entries in each eigenvector are called the loadings of the variables on the component. The loadings give us an idea how important each variable is to each component. For example, it seems that the third variable in our dataset (Petal Length) is dominating the first principal component. This should not come as too much of a shock - that variable had (by far) the largest amount of variation of the four. In order to capture the most amount of variance in a single dimension, we should certainly be considering this variable strongly. The variable with the next largest variance, Sepal Length, dominates the second principal component.
Note: Had Petal Length and Sepal Length been correlated, they would not have dominated separate principal components, they would have shared one. These two variables are not correlated and thus their variation cannot be captured along the same direction.
14.0.3 Scores and PCA Projection
Lets plot the projection of the four-dimensional iris data onto the two dimensional space spanned by the first 2 principal components. To do this, we need coordinates. These coordinates are commonly called scores in statistical texts. We can find the coordinates of the data on the principal components by solving the system \[\mathbf{X}=\mathbf{A}\mathbf{V}^T\] where \(\mathbf{X}\) is our original iris data (centered to have mean = 0) and \(\mathbf{A}\) is a matrix of coordinates in the new principal component space, spanned by the eigenvectors in \(\mathbf{V}\).
Solving this system is simple enough - since \(\mathbf{V}\) is an orthogonal matrix. Let’s confirm this:
eig$vectors %*% t(eig$vectors)## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length 1.000000e+00 4.163336e-17 -2.775558e-17 -2.775558e-17
## Sepal.Width 4.163336e-17 1.000000e+00 1.665335e-16 1.942890e-16
## Petal.Length -2.775558e-17 1.665335e-16 1.000000e+00 -2.220446e-16
## Petal.Width -2.775558e-17 1.942890e-16 -2.220446e-16 1.000000e+00t(eig$vectors) %*% eig$vectors## [,1] [,2] [,3] [,4]
## [1,] 1.000000e+00 -2.289835e-16 0.000000e+00 -1.110223e-16
## [2,] -2.289835e-16 1.000000e+00 2.775558e-17 -1.318390e-16
## [3,] 0.000000e+00 2.775558e-17 1.000000e+00 1.110223e-16
## [4,] -1.110223e-16 -1.318390e-16 1.110223e-16 1.000000e+00We’ll have to settle for precision at 15 decimal places. Close enough!
So to find the scores, we simply subtract the means from our original variables to create the data matrix \(\mathbf{X}\) and compute \[\mathbf{A}=\mathbf{X}\mathbf{V}\]
# The scale function centers and scales by default
X=scale(iris[1:4],center=TRUE,scale=FALSE)
# Create data.frame from matrix for plotting purposes.
scores=data.frame(X %*% eig$vectors)
# Change default variable names
colnames(scores)=c("Prin1","Prin2","Prin3","Prin4")
# Print coordinates/scores of first 10 observations
scores[1:10, ]## Prin1 Prin2 Prin3 Prin4
## 1 -2.684126 -0.31939725 -0.02791483 0.002262437
## 2 -2.714142 0.17700123 -0.21046427 0.099026550
## 3 -2.888991 0.14494943 0.01790026 0.019968390
## 4 -2.745343 0.31829898 0.03155937 -0.075575817
## 5 -2.728717 -0.32675451 0.09007924 -0.061258593
## 6 -2.280860 -0.74133045 0.16867766 -0.024200858
## 7 -2.820538 0.08946138 0.25789216 -0.048143106
## 8 -2.626145 -0.16338496 -0.02187932 -0.045297871
## 9 -2.886383 0.57831175 0.02075957 -0.026744736
## 10 -2.672756 0.11377425 -0.19763272 -0.056295401To this point, we have simply computed coordinates (scores) on a new set of axis (principal components, eigenvectors, loadings). These axis are orthogonal and are aligned with the directions of maximal variance in the data. When we consider only a subset of principal components (like 2 components accounting for 97% of the variance), then we are projecting the data onto a lower dimensional space. Generally, this is one of the primary goals of PCA: Project the data down into a lower dimensional space (onto the span of the principal components) while keeping the maximum amount of information (i.e. variance).
Thus, we know that almost 98% of the data’s variance can be seen in two-dimensions using the first two principal components. Let’s go ahead and see what this looks like:
plot(scores$Prin1, scores$Prin2,
main="Data Projected on First 2 Principal Components",
xlab="First Principal Component",
ylab="Second Principal Component",
col=c("red","green3","blue")[iris$Species])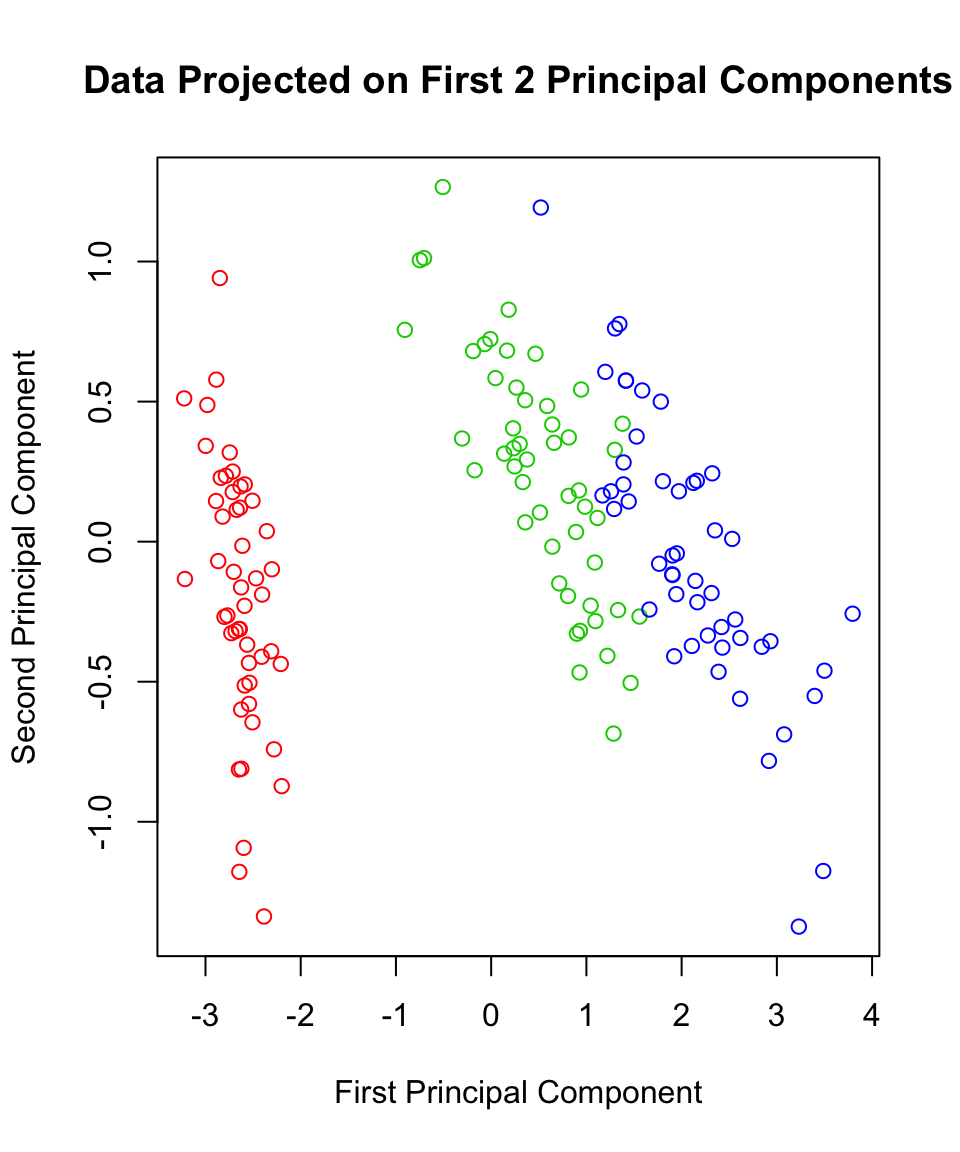
14.0.4 PCA functions in R
irispca=prcomp(iris[1:4])
# Variance Explained
summary(irispca)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 2.0563 0.49262 0.2797 0.15439
## Proportion of Variance 0.9246 0.05307 0.0171 0.00521
## Cumulative Proportion 0.9246 0.97769 0.9948 1.00000# Eigenvectors:
irispca$rotation## PC1 PC2 PC3 PC4
## Sepal.Length 0.36138659 -0.65658877 0.58202985 0.3154872
## Sepal.Width -0.08452251 -0.73016143 -0.59791083 -0.3197231
## Petal.Length 0.85667061 0.17337266 -0.07623608 -0.4798390
## Petal.Width 0.35828920 0.07548102 -0.54583143 0.7536574# Coordinates of first 10 observations along PCs:
irispca$x[1:10, ]## PC1 PC2 PC3 PC4
## [1,] -2.684126 -0.31939725 0.02791483 0.002262437
## [2,] -2.714142 0.17700123 0.21046427 0.099026550
## [3,] -2.888991 0.14494943 -0.01790026 0.019968390
## [4,] -2.745343 0.31829898 -0.03155937 -0.075575817
## [5,] -2.728717 -0.32675451 -0.09007924 -0.061258593
## [6,] -2.280860 -0.74133045 -0.16867766 -0.024200858
## [7,] -2.820538 0.08946138 -0.25789216 -0.048143106
## [8,] -2.626145 -0.16338496 0.02187932 -0.045297871
## [9,] -2.886383 0.57831175 -0.02075957 -0.026744736
## [10,] -2.672756 0.11377425 0.19763272 -0.056295401All of the information we computed using eigenvectors aligns with what we see here, except that the coordinates/scores and the loadings of Principal Component 3 are of the opposite sign. In light of what we know about eigenvectors representing directions, this should be no cause for alarm. The prcomp function arrived at the unit basis vector pointing in the negative direction of the one we found directly from the eig function - which should negate all the coordinates and leave us with an equivalent mirror image in all of our projections.
14.0.5 The Biplot
One additional feature that R users have created is the biplot. The PCA biplot allows us to see where our original variables fall in the space of the principal components. Highly correlated variables will fall along the same direction (or exactly opposite directions) as a change in one of these variables correlates to a change in the other. Uncorrelated variables will appear further apart. The length of the variable vectors on the biplot tell us the degree to which variability in variable is explained in that direction. Shorter vectors have less variability than longer vectors. So in the biplot below, petal width and petal length point in the same direction indicating that these variables share a relatively high degree of correlation. However, the vector for petal width is much shorter than that of petal length, which means you can expect a higher degree of change in petal length as you proceed to the right along PC1. PC1 explains more of the variance in petal length than it does petal width. If we were to imagine a third PC orthogonal to the plane shown, petal width is likely to exist at much larger angle off the plane - here, it is being projected down from that 3-dimensional picture.
biplot(irispca, col = c("gray", "blue"))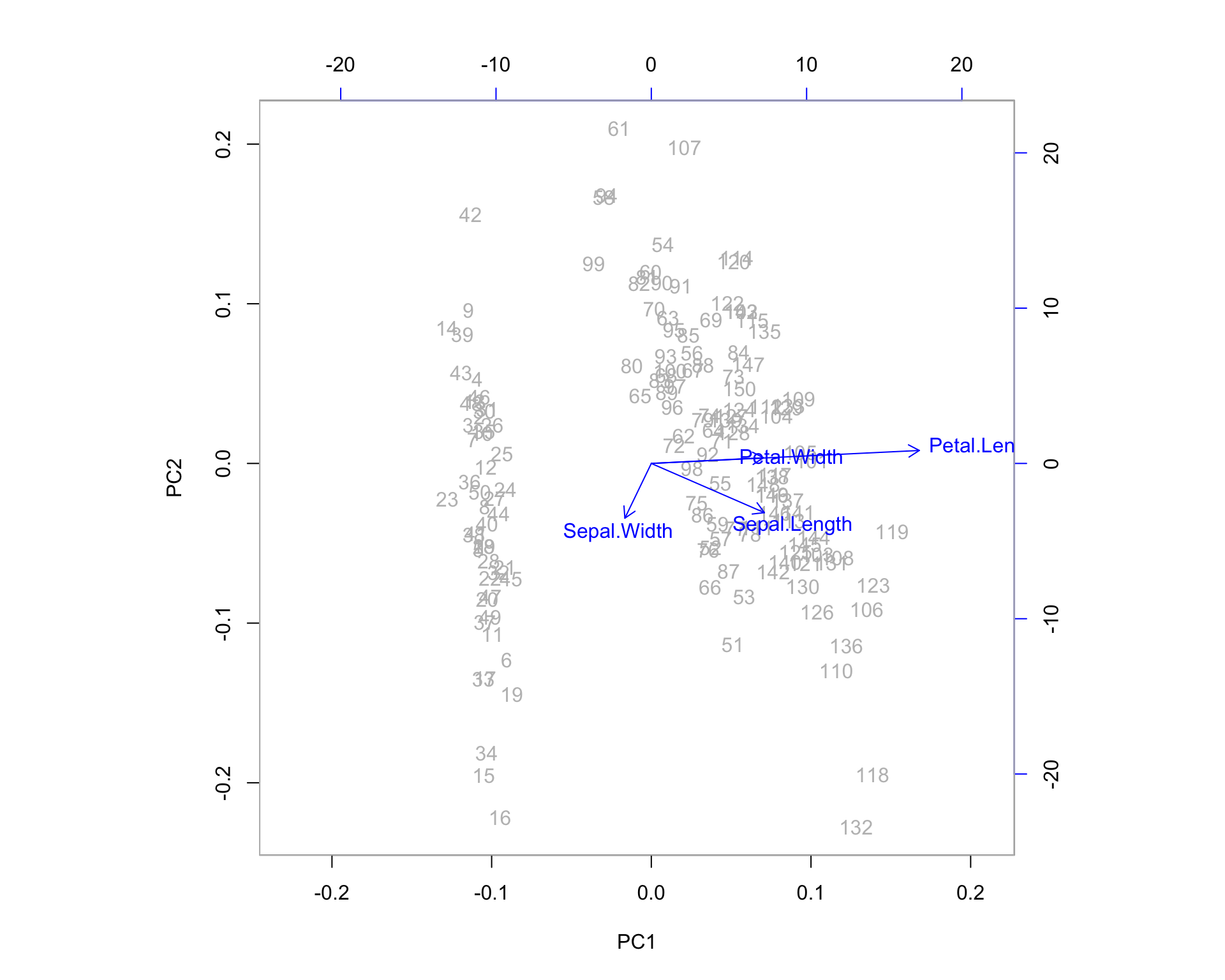
We can examine some of the outlying observations to see how they align with these projected variable directions. It helps to compare them to the quartiles of the data. Also keep in mind the direction of the arrows in the plot. If the arrow points down then the positive direction is down - indicating observations which are greater than the mean. Let’s pick out observations 42 and 132 and see what the actual data points look like in comparison to the rest of the sample population.
summary(iris[1:4])## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
## Median :5.800 Median :3.000 Median :4.350 Median :1.300
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500# Consider orientation of outlying observations:
iris[42, ]## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 42 4.5 2.3 1.3 0.3 setosairis[132, ]## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 132 7.9 3.8 6.4 2 virginica14.1 Variable Clustering with PCA
The direction arrows on the biplot are merely the coefficients of the original variables when combined to make principal components. Don’t forget that principal components are simply linear combinations of the original variables.
For example, here we have the first principal component (the first column of \(\V\)), \(\mathbf{v}_1\) as:
eig$vectors[,1]## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 0.36138659 -0.08452251 0.85667061 0.35828920This means that the coordinates of the data along the first principal component, which we’ll denote here as \(PC_1\) are given by a simple linear combination of our original variables after centering (for covariance PCA) or standardization (for correlation PCA)
\[PC_1 = 0.36Sepal.Length-0.08Sepal.Width+0.85Petal.Length +0.35Petal.Width\] the same equation could be written for each of the vectors of coordinates along principal components, \(PC_1,\dots, PC_4\).
Essentially, we have a system of equations telling us that the rows of \(\V^T\) (i.e. the columns of \(\V\)) give us the weights of each variable for each principal component: \[\begin{equation} \tag{14.1} \begin{bmatrix} PC_1\\PC_2\\PC_3\\PC_4\end{bmatrix} = \mathbf{V}^T\begin{bmatrix}Sepal.Length\\Sepal.Width\\Petal.Length\\Petal.Width\end{bmatrix} \end{equation}\]
Thus, if want the coordinates of our original variables in terms of Principal Components (so that we can plot them as we do in the biplot) we need to look no further than the rows of the matrix \(\mathbf{V}\) as \[\begin{equation} \tag{14.2} \begin{bmatrix}Sepal.Length\\Sepal.Width\\Petal.Length\\Petal.Width\end{bmatrix} =\mathbf{V}\begin{bmatrix} PC_1\\PC_2\\PC_3\\PC_4\end{bmatrix} \end{equation}\]
means that the rows of \(\mathbf{V}\) give us the coordinates of our original variables in the PCA space. The transition from Equation (14.1) to Equation (14.2) is provided by the orthogonality of the eigenvectors per Theorem 13.1.
#First entry in each eigenvectors give coefficients for Variable 1:
eig$vectors[1,]## [1] 0.3613866 -0.6565888 -0.5820299 0.3154872\[Sepal.Length = 0.361 PC_1 - 0.657 PC_2 - 0.582 PC_3 + 0.315 PC_4\] You can see this on the biplot. The vector shown for Sepal.Length is (0.361, -0.656), which is the two dimensional projection formed by throwing out components 3 and 4.
Variables which lie upon similar directions in the PCA space tend to change together in a similar fashion. We might consider Petal.Width and Petal.Length as a cluster of variables because they share a direction on the biplot, which means they represent much of the same information (the underlying construct being the “size of the petal” in this case).
14.1.1 Correlation PCA
We can complete the same analysis using the correlation matrix. I’ll leave it as an exercise to compute the Principal Component loadings and scores and variance explained directly from eigenvectors and eigenvalues. You should do this and compare your results to the R output. (Beware: you must transform your data before solving for the scores. With the covariance version, this meant centering - for the correlation version, this means standardization as well)
irispca2=prcomp(iris[1:4], cor=TRUE)## Warning: In prcomp.default(iris[1:4], cor = TRUE) :
## extra argument 'cor' will be disregardedsummary(irispca2)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 2.0563 0.49262 0.2797 0.15439
## Proportion of Variance 0.9246 0.05307 0.0171 0.00521
## Cumulative Proportion 0.9246 0.97769 0.9948 1.00000irispca2$rotation## PC1 PC2 PC3 PC4
## Sepal.Length 0.36138659 -0.65658877 0.58202985 0.3154872
## Sepal.Width -0.08452251 -0.73016143 -0.59791083 -0.3197231
## Petal.Length 0.85667061 0.17337266 -0.07623608 -0.4798390
## Petal.Width 0.35828920 0.07548102 -0.54583143 0.7536574irispca2$x[1:10,]## PC1 PC2 PC3 PC4
## [1,] -2.684126 -0.31939725 0.02791483 0.002262437
## [2,] -2.714142 0.17700123 0.21046427 0.099026550
## [3,] -2.888991 0.14494943 -0.01790026 0.019968390
## [4,] -2.745343 0.31829898 -0.03155937 -0.075575817
## [5,] -2.728717 -0.32675451 -0.09007924 -0.061258593
## [6,] -2.280860 -0.74133045 -0.16867766 -0.024200858
## [7,] -2.820538 0.08946138 -0.25789216 -0.048143106
## [8,] -2.626145 -0.16338496 0.02187932 -0.045297871
## [9,] -2.886383 0.57831175 -0.02075957 -0.026744736
## [10,] -2.672756 0.11377425 0.19763272 -0.056295401plot(irispca2$x[,1],irispca2$x[,2],
main="Data Projected on First 2 Principal Components",
xlab="First Principal Component",
ylab="Second Principal Component",
col=c("red","green3","blue")[iris$Species])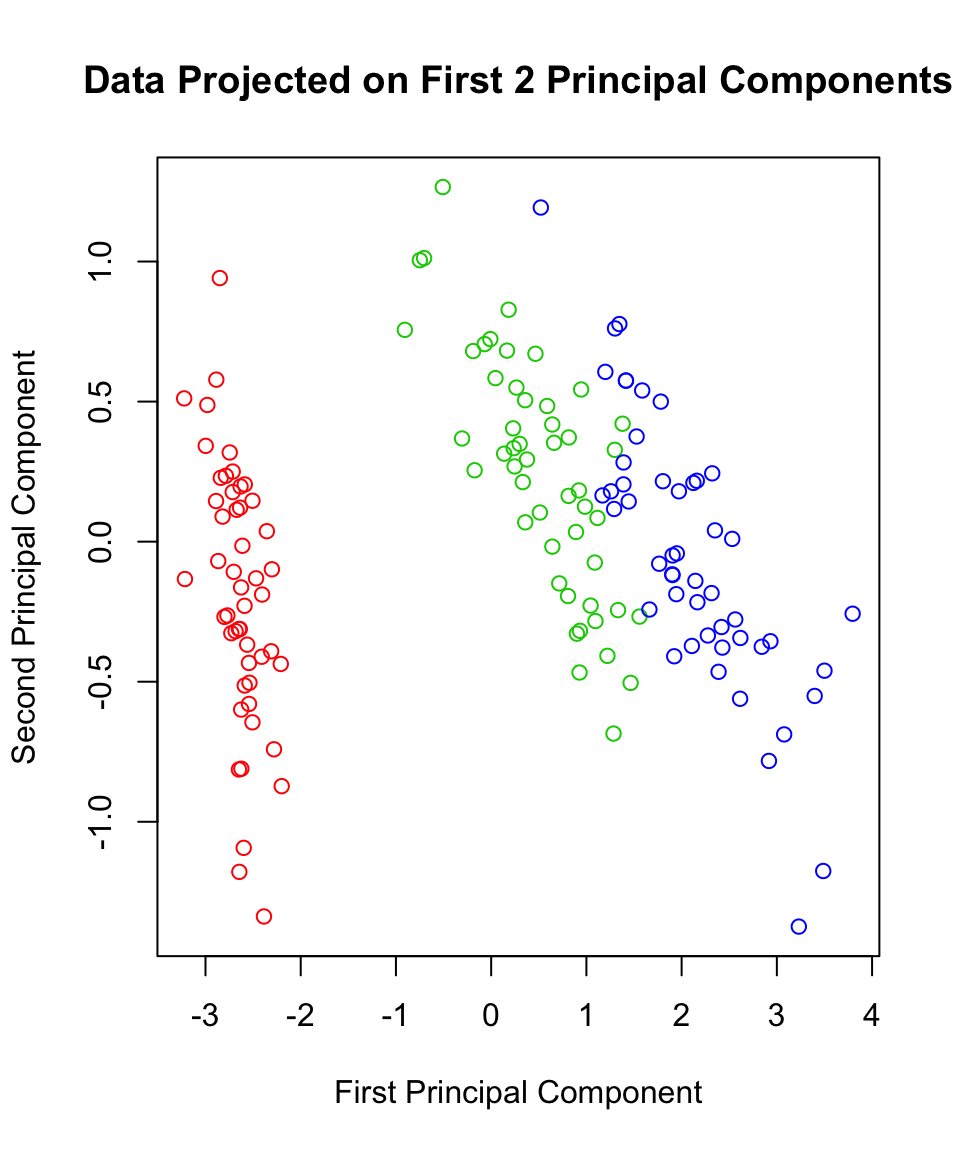
biplot(irispca2)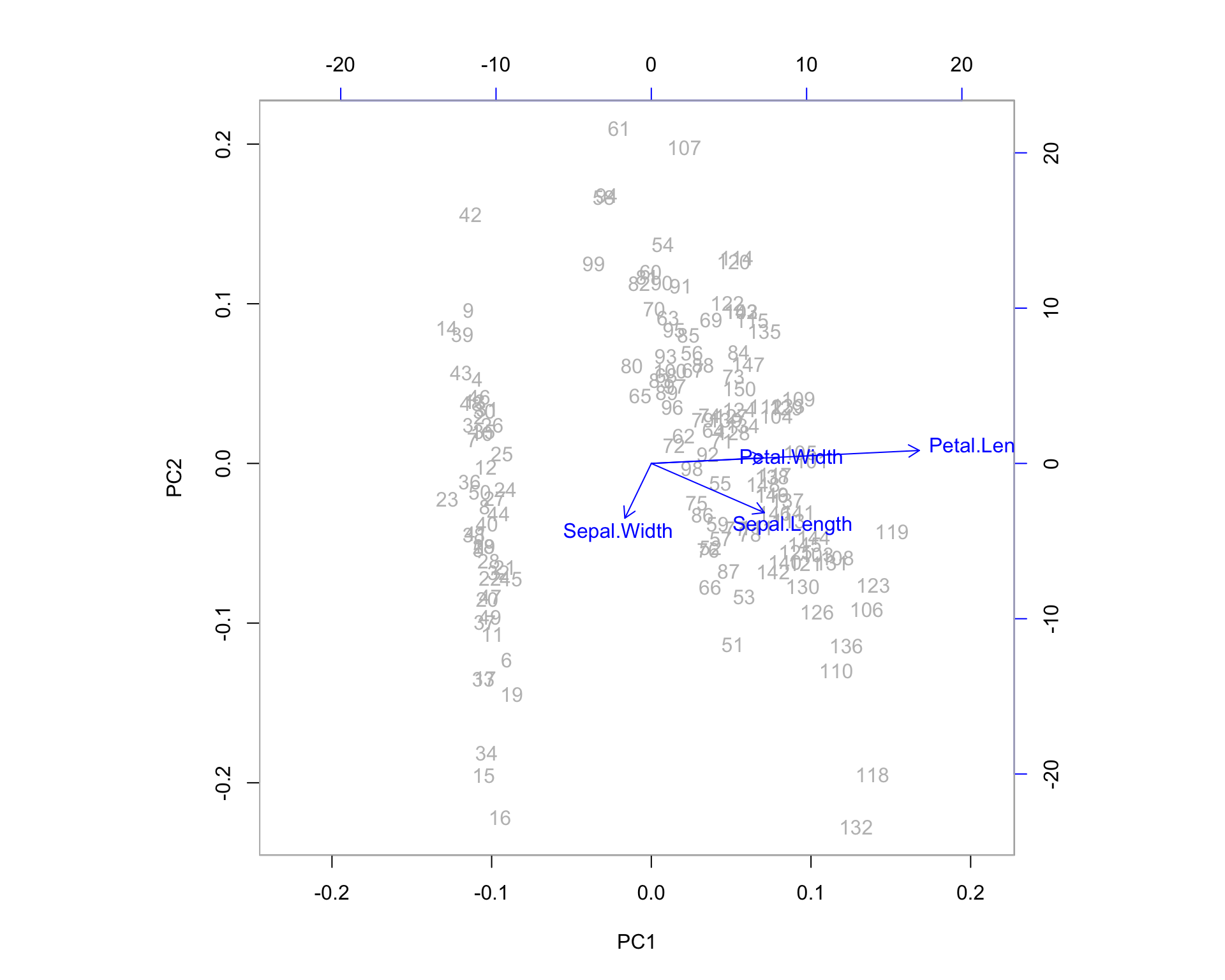
Here you can see the direction vectors of the original variables are relatively uniform in length in the PCA space. This is due to the standardization in the correlation matrix. However, the general message is the same: Petal.Width and Petal.Length Cluster together, and many of the same observations appear “on the fray” on the PCA space - although not all of them!
14.1.2 Which Projection is Better?
What do you think? It depends on the task, and it depends on the data. One flavor of PCA is not “better” than the other. Correlation PCA is appropriate when the scales of your attributes differ wildly, and covariance PCA would be inappropriate in that situation. But in all other scenarios, when the scales of our attributes are roughly the same, we should always consider both dimension reductions and make a decision based upon the resulting output (variance explained, projection plots, loadings).
For the iris data, The results in terms of variable clustering are pretty much the same. For clustering/classifying the 3 species of flowers, we can see better separation in the covariance version.
14.1.3 Beware of biplots
Be careful not to draw improper conclusions from biplots. Particularly, be careful about situations where the first two principal components do not summarize the majority of the variance. If a large amount of variance is captured by the 3rd or 4th (or higher) principal components, then we must keep in mind that the variable projections on the first two principal components are flattened out versions of a higher dimensional picture. If a variable vector appears short in the 2-dimensional projection, it means one of two things:
- That variable has small variance
- That variable appears to have small variance when depicted in the space of the first two principal components, but truly has a larger variance which is represented by 3rd or higher principal components.
Let’s take a look at an example of this. We’ll generate 500 rows of data on 4 nearly independent normal random variables. Since these variables are uncorrelated, we might expect that the 4 orthogonal principal components will line up relatively close to the original variables. If this doesn’t happen, then at the very least we can expect the biplot to show little to no correlation between the variables. We’ll give variables \(2\) and \(3\) the largest variance. Multiple runs of this code will generate different results with similar implications.
means=c(2,4,1,3)
sigmas=c(7,9,10,8)
sample.size=500
data=mapply(function(mu,sig){rnorm(mu,sig, n=sample.size)},mu=means,sig=sigmas)
cor(data)## [,1] [,2] [,3] [,4]
## [1,] 1.000000000 0.004631157 -0.001606022 -0.01300897
## [2,] 0.004631157 1.000000000 -0.047758870 0.04828778
## [3,] -0.001606022 -0.047758870 1.000000000 0.05867241
## [4,] -0.013008971 0.048287779 0.058672408 1.00000000pc=prcomp(data,scale=TRUE)
summary(pc)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 1.0298 1.0221 0.9995 0.9465
## Proportion of Variance 0.2651 0.2612 0.2498 0.2240
## Cumulative Proportion 0.2651 0.5263 0.7760 1.0000pc$rotation## PC1 PC2 PC3 PC4
## [1,] 0.16990220 0.006373112 -0.98137245 0.08944683
## [2,] -0.01667324 -0.835064957 -0.05814887 -0.54681553
## [3,] -0.68171582 0.407578128 -0.16857926 -0.58371623
## [4,] -0.71142026 -0.369467144 -0.07146923 0.59352118biplot(pc)
Figure 14.1: BiPlot of Iris Data
Obviously, the wrong conclusion to make from this biplot is that Variables 1 and 4 are correlated. Variables 1 and 4 do not load highly on the first two principal components - in the whole 4-dimensional principal component space they are nearly orthogonal to each other and to variables 1 and 2. Thus, their orthogonal projections appear near the origin of this 2-dimensional subspace.
The morals of the story:
- Always corroborate your results using the variable loadings and the amount of variation explained by each variable.
- When a variable shows up near the origin in a biplot, it is generally not well represented by your two-dimensional approximation of the data.